Introducing whatip.info. A very very simple Go program behind an NGINX server to resolve and return the remote IPv4 (and soon IPv6) address. My motivation behind it is dead simple: I need that exact functionality from something I know I control. Prior to this, I was using several alternatives: ifconfig.me ifconfig.co icanhazip.com All work great but I wished to curl something of my own making. Thus whatip.info was born. Here’s the code: ...
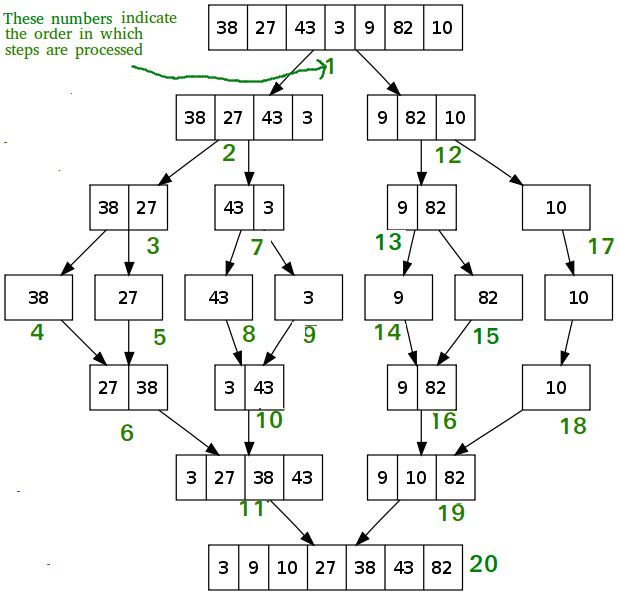
Here’s my implementation of the Mergesort algorithm in Golang package main import ( "fmt" "io/ioutil" "math/rand" "strconv" "strings" "time" ) func main() { start := time.Now() arr := randArr(20) // Merge sort array fmt.Println("\n Sorted \n", mergeSort(arr)) fmt.Println("Sorted in: ", time.Since(start)) } // Function to generate random array func randArr(size int) []int { arr := make([]int, size, size) rand.Seed(time.Now().UnixNano()) for i := 0; i < size; i++ { arr[i] = rand.Intn(99) } return arr } // Merge sort accepts an array and recursively sorts it func mergeSort(arr []int) []int { if len(arr) < 2 { return arr } middle := (len(arr)) / 2 return merge(mergeSort(arr[:middle]), mergeSort(arr[middle:])) } // Merges two arrays into one func merge(left, right []int) []int { var sortedArr []int // Check for inversions while array for len(left) > 0 && len(right) > 0 { if left[0] <= right[0] { sortedArr = append(sortedArr, left[0]) left = left[1:] // Just like shift(), remove first and return slice } else { sortedArr = append(sortedArr, right[0]) right = right[1:] // Just like shift(), remove first and return slice } } // Append to sortedArr if no inversions and for len(left) > 0 { sortedArr = append(sortedArr, left[0]) left = left[1:] // Just like shift(), remove first and return slice } for len(right) > 0 { sortedArr = append(sortedArr, right[0]) right = right[1:] // Just like shift(), remove first and return slice } return sortedArr } and here’s in Javascript ...
Rather than using the popular joke about recursion (see bottom), I’ll reference a very peculiar adage which makes use of this particular mental model: The Hogstadter’s Law, states that: It always takes longer than you expect, even when you take into account Hofstadter’s Law. See what happened there? The law is a self-referential adage, that tries to describe the widely experienced difficulty of accuratelly estimate the time it will take to complete tasks of substancial complexity. ...